reading-notes-ma

---

Project maintained by mohnalkhateeb Hosted on GitHub Pages — Theme by mattgraham

Implementation: Linked Lists

• Big O: Analysis of Algorithm Efficiency

  Big O(oh) notation is used to describe the efficiency of an algorithm or function. This efficiency is evaluated based on 2 factors:

  • Running Time complexity : The amount of time a function needs to complete.

  • Memory Space complexity : The amount of memory resources a function uses to store data and instructions.

  • we should consider 4 Key Areas for analysis:

  • Input Size

    Input Size refers to the size of the parameter values that are read by the algorithm. This does not simply refer to the number of parameters an algorithm reads, but takes into account the size of each parameter value as well.

    • We will use the letter n to refer to the Input Size value.

    • The higher this number, the more likely there will be an increase to Running Time and Memory Space.

  • Units of Measurement

    In order to quantify the Running Time in our analysis, we will consider Three Measurements of time:

    • 1- The time in milliseconds from the start of a function execution until it ends.
    • 2- The number of operations that are executed.
    • 3- The number of “Basic Operations” that are executed.

    In order to quantify Memory Space, we can consider Four Sources of Memory Usage during function run-time:

    • 1- The amount of space needed to hold the code for the algorithm.
    • 2- The amount of space needed to hold the input data.
    • 3- The amount of space needed for the output data.
    • 4- The amount of space needed to hold working space during the calculation.

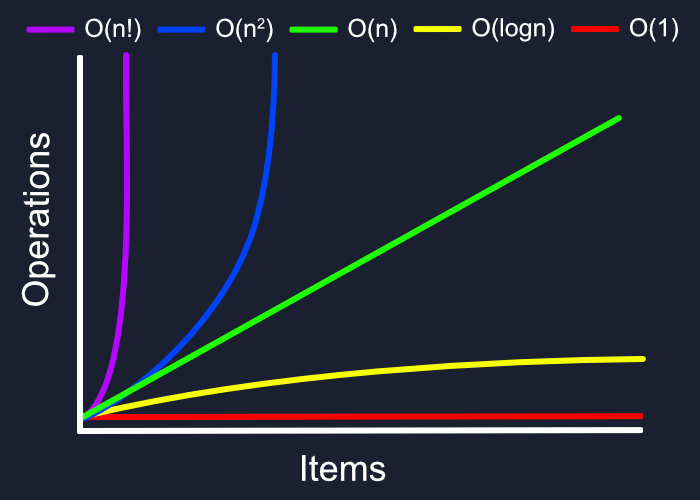
  • Orders of Growth

    We can describe overall efficiency by using the input size n and measuring the overall Units of Space and Time required for the given input size n. As the value of n grows, the Order of Growth represents the increase in Running Time or Memory Space

    • Constant Complexity :

      means that no matter what inputs are thrown at our algorithm, it always uses the same amount of time or space. The number 1 is used to represent a constant value. The actual number of units will most likely be greater than 1, we round this number down to 1 to represent our estimate of complexity that is independant of n.

    • Logarithmic Complexity :

      represents a function that sees a decrease in the rate of complexity growth, the greater our value of n. This can be seen when we are performing calculations on sorted data. For instance if we are searching for a value in a sorted array, we have an idea of where to start searching instead of starting at the first index moving toward n. foe example binary search

    • Linear Complexity

      example : simple loop

    • Linearithmic Complexity

      is used to describe a growth rate of n by lgn. This represents complexity that grows with n, but also by lgn. Linearithmic functions grow faster than input size n, but not by much. This can be seen in divide and conquer algorithms such as the Merge Sort have linearithmic complexity growth rates. example is sort Algorithm

    • Quadratic Complexity

      example : nested loop

    • Exponential Complexity

      The fibonacci sequence is a popular case for exponential complexity growth

    • Factorial Complexity

      means that the our space and time requirements grow extremely fast, relative to our input size. For example, how many ways could you arrange a deck of cards?

    

  • Best Case, Worst Case, and Average Case

    • Worst Case:

      The efficiency for the worst possible input of size n :This case runs the longest for all possible inputs of n. This assumes that if we were sorting values, inputs are completely unsorted and searched values either don’t exist or are at the last to be searched.

    • Best Case:

      The efficiency for the best possible input of size n . This case runs the quickest for all possible inputs of n. In the case of sorting, this assumes that values are sorted, and so searched-for values are easy to find.

    • Average Case:

      The efficiency for a “typical” or “random” input of size n. The average case makes a typical assumption about the possible inputs of size ‘n’ and how they might affect efficiency. This is NOT the best case and worst case averaged together.

• Linked List

  • What is a Linked List

    A Linked List is a sequence of Nodes that are connected/linked to each other. The most defining feature of a Linked List is that each Node references the next Node in the link. There are two types of Linked List - Singly and Doubly

  • Adding a Node

    

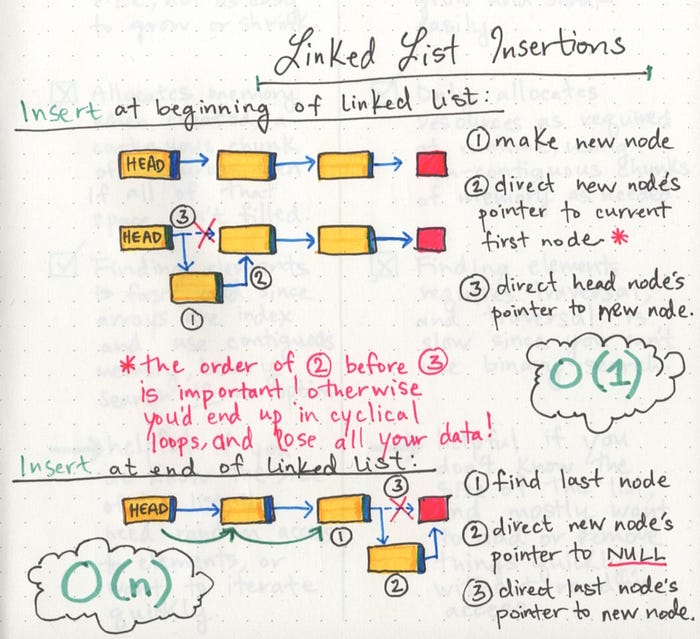
  • Print Out Nodes

    Printing out all of the nodes in a Linked List is very similar to what we did in the Includes() method. This is because we are leveraging our Current node and a while loop to traverse through the existing linked list.